One Dimensional Motion
Time and Distance
By one dimension we mean that the body is moving only in one plane and in a straight line. Like if we roll a marble on a flat table, and if we roll it in a straight line (not easy!), then it would be undergoing one-dimensional motion. There are four variables which put together in an equation can describe this motion. These are Initial Velocity (u); Final Velocity (v), Acceleration (a), Distance Traveled (s) and Time elapsed (t). The equations which tell us the relationship between these variables are as given below.
v = u + at
s = ut + 1/2 at 2
Two and Three Dimensional Motion
Scalar or Vector?
To explain the difference we use two words: 'magnitude' and 'direction'. By magnitude we mean how much of the quantity is there. By direction we mean is this quantity having a direction which defines it. Physical quantities which are completely specified by just giving out there magnitude are known as scalars. Examples of scalar quantities are distance, mass, speed, volume, density, temperature etc. Other physical quantities cannot be defined by just their magnitude. To define them completely we must also specify their direction. Examples of these are velocity, displacement, acceleration, force, torque, momentum etc.
Parallelogram law of vector addition
If we were to represent two vectors magnitude and direction by two adjacent sides of a parallelogram. The resultant can then be represented in magnitude and direction by the diagonal. This diagonal is the one which passes through the point of intersection of these two sides.
Resolution of a Vector
It is often necessary to split a vector into its components. Splitting of a vector into its components is called resolution of the vector. The original vector is the resultant of these components. When the components of a vector are at right angle to each other they are called the rectangular components of a vector.
Rectangular Components of a Vector
As the rectangular components of a vector are perpendicular to each other, we can do mathematics on them. This allows us to solve many real life problems. After all the best thing about physics is that it can be used to solve real world problems.
Note: We will show all vector quantities in bold. For example A will be scalar quantity and A will be a vector quantity.
Let A x and A y be the rectangular components of a vector A
then
A = A x + A y this means that vector A is the resultant of vectors A x and A y
A is the magnitude of vector A and similarly A x and A y are the magnitudes of vectors A x and A y
As we are dealing with rectangular components which are at right angles to each other. We can say that:
A = (A x + A y) 1/2
Similarly the angle Q which the vector A makes with the horizontal direction will be
Q = tan -1 (A x / A y)
Laws of Motion
Newton's laws of motion
Through Newton's second law, which states: The acceleration of a body is directly proportional to the net unbalanced force and inversely proportional to the body's mass, a relationship is established between
Force (F), Mass (m) and acceleration (a). This is of course a wonderful relation and of immense usefulness.
Knowing any two of the quantities automatically gives you the third !!
Momentum
Momentum (p) is the quantity of motion in a body. A heavy body moving at a fast velocity is difficult to stop. A light body at a slow speed, on the other hand can be stopped easily. So momentum has to do with both mass and velocity.
Often physics problems deal with momentum before and after a collision. In such cases the total momentum of the bodies before collision is taken as equal to the total momentum of the bodies after collision. That is to say: momentum is conserved.
Impulse
This is the change in the momentum of a body caused over a very short time. Let m be the mass and v and u the final and initial velocities of a body.
Work, Energy and Power
Work and energy
As we know from the law of conservation of energy: energy is always conserved.
Work is the product of force and the distance over which it moves. Imagine you are pushing a heavy box across the room. The further you move the more work you do! If W is work, F the force and x the distance then.
W = Fx
Energy comes in many shapes. The ones we see over here are kinetic energy (KE) and potential energy (PE)
Transitional KE = ½ mv 2
Rotational KE = ½ Iw 2
here I is the moment of inertia of the object (a simple manner in which one can understand moment of inertia is to consider it to be similar to mass in transitional KE) and w is angular velocity
where h is the height of the object
Elastic PE = ½ k L 2
where k is the spring constant ( it gives how much a spring will stretch for a unit force) and L is the length of the spring.
Power
Power (P) is work( W) done in unit time (t).
P = W/t
as work and energy (E) are same it follows power is also energy consumed or generated per unit time.
P = E/t
In measuring power Horsepower is a unit which is in common use. However in physics we use Watt. So the first thing to do in solving any problem related to power is to convert horsepower to Watts. 1 horsepower (hp) = 746 Watts
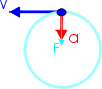
Circular Motion
In the diagram v is the tangential velocity of the object. a is the centripetal (acting towards the center of the circle) acceleration and F is the centripetal force. r is the radius of the circle and m is mass of the object.
as work and energy (E) are same it follows power is also energy consumed or generated per unit time.
a = v 2 / r
F = ma = mv 2/r
Gravitation
Kepler's Laws
Towards the end of the sixteenth century, Tycho Brahe collected a huge amount of data giving precise measurements of the position of planets. Johannes Kepler, after a detailed analysis of the measurements announced three laws in 1619.
1. The orbit of each planet is an ellipse which has the Sun at one of its foci.
2. Each planet moves in such a way that the (imaginary) line joining it to the Sun sweeps out equal areas in equal times.
3. The squares of the periods of revolution of the planets about the Sun are proportional to the cubes of their mean distances from it.
Newton's law of universal gravitation
About fifty years after Kepler announced the laws now named after him, Isaac Newton showed that every particle in the Universe attracts every other with a force which is proportional to the products of their masses and inversely proportional to the square of their separation.
Hence:
If F is the force due to gravity, g the acceleration due to gravity, G the Universal Gravitational Constant (6.67x10-11 N.m2/kg2), m the mass and r the distance between two objects. Then
F = G m 1 m 2 / r 2
Acceleration due to gravity outside the Earth
Here let r represent the radius of the point inside the earth. The formula for finding out the acceleration due to gravity at this point becomes:
g' = ( r / re )g
In both the above formulas, as expected, g' becomes equal to g when r = re.
Properties of Matter
Density
The mass of a substance contained in unit volume is its density (D).
D = m/V
Measuring of densities of substances is easier if we compare them with the density of some other substance of know density. Water is used for this purpose. The ratio of the density of the substance to that of water is called thepecific Gravity (SG)S of the substance.
SG = D substance / D water
The density of water is 1000 kg/m 3
Pressure
Pressure (P) is Force (F) per unit area (A)
P = F/A
Specific Heat
You may have noticed that metals, for example copper, heat faster than water. You would require 4186 J of heat to raise the temperature of water by 1 degree Celsius. On the other hand 1 kg of copper would zoom to this temperature after it receives only 387 J of heat. It is known that every substance has a unique value of amount of heat required to change the temperature of 1 kg of it by 1 degree Celsius. This number is referred to as the specific heat of the substance. Let Q be the heat transferred to m kg of a substance, thereby changing its temperature by dT. The specific heat c of the substance is defined as
c = Q/mdt
Juggle the expression, and we get the heat transferred from a body to its surroundings or the other way around. This is given by.
Q = m c dT
For example the heat required to increase the temperature of half a kg of water by 3 degrees Celsius can be determined using this formula. Here m, mass of water is 0.5 kg and the dt, the temperature rise = 3 deg C and we know the specific heat of water is 4186 J/kg. So here the heat required will be
Q = 0.5 x 4186 x 3 =6280 J
It is as simple as that !!
he table below gives the specific heat of some common substances
| J/kg. o C | cal/g. o C |
| Aluminium | 900 | 0.215 |
| Copper | 387 | 0.0924 |
| Glass | 837 | 0.200 |
| Gold | 129 | 0.0308 |
| Ice | 2090 | 0.500 |
| Iron | 448 | 0.107 |
| Silver | 234 | 0.056 |
| Steam | 2010 | 0.480 |
| Water | 4186 | 1.00 |
Electricity
Electricity
According to Ohm's Law electric potential difference(V) is directly proportional to the product of the current(I) times the resistance(R).
V = I R
The relationship between power (P) and current and voltage is
P = I V
Using the equations above we can also write
P = V 2 / R
and
P = I 2 R
Resistance of Resistors in Series
The equivalent resistance (R eq) of a set of; resistors connected in series is
R eq = R 1 + R 2 + R 3 + - - -
Resistance of Resistors in Parallel
The equivalent resistance (R eq) of a set of resistors connected in parallel is
1/R eq = 1/R 1 + 1/R 2 + 1/R 3 + - - -
| 
No comments:
Post a Comment